Number of Enclaves

Problem

You are given an m x n binary matrix grid, where 0 represents a sea cell and 1 represents a land cell.

A move consists of walking from one land cell to another adjacent (4-directionally) land cell or walking off the boundary of the grid.

Return the number of land cells in grid for which we cannot walk off the boundary of the grid in any number of moves.

Example 1:

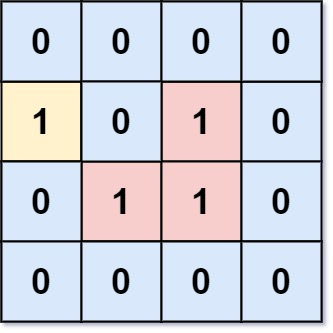
Input: grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] Output: 3 Explanation: There are three 1s that are enclosed by 0s, and one 1 that is not enclosed because its on the boundary.

Example 2:

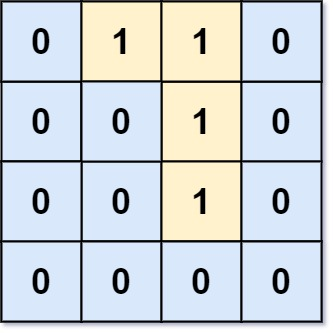
Input: grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]] Output: 0 Explanation: All 1s are either on the boundary or can reach the boundary.

Solution

class Solution:
    def numEnclaves(self, grid: List[List[int]]) -> int:
        not_reach_boundary = 0
 
        y_len, x_len = len(grid), len(grid[0])
 
        # Cleanup borders
        for y in range(y_len):
            for x in range(x_len):
                if y == 0 or x == 0 or y == (y_len - 1) or x == (x_len - 1):
                    self.clean_up_dfs(x, y, grid)
 
        for y in range(y_len):
            for x in range(x_len):
                if grid[y][x] == 1:
                    not_reach_boundary += 1
 
        return not_reach_boundary
 
    def clean_up_dfs(self, x, y, grid):
        if x < 0 or y < 0 or y == len(grid) or x == len(grid[0]) or grid[y][x] == 0:
            return
 
        grid[y][x] = 0
 
        self.clean_up_dfs(x - 1, y, grid)
        self.clean_up_dfs(x + 1, y, grid)
        self.clean_up_dfs(x, y - 1, grid)
        self.clean_up_dfs(x, y + 1, grid)

Explanation

This solution solves the “Number of Enclaves” problem by first “cleaning” or removing any land cells (represented as 1’s) that can reach the grid’s boundary, and then counting the remaining land cells that form enclaves. Here’s a detailed breakdown:

1. Overall Idea

• Objective:
  Count land cells (value 1) that are completely surrounded by water (value 0), meaning they cannot reach any boundary of the grid.

• Approach:
  Use depth-first search (DFS) to eliminate (or “sink”) all land cells that are connected to any border cell. After this elimination, any remaining land cell is an enclave.

---

2. Cleanup Phase (Border Traversal and DFS)

• Iterating Through the Border:
  The solution first calculates the grid dimensions with y_len (number of rows) and x_len (number of columns). It then iterates over every cell on the border:

  • The condition if y == 0 or x == 0 or y == (y_len - 1) or x == (x_len - 1) identifies border cells.

  • For each border cell, it calls self.clean_up_dfs(x, y, grid).

• Purpose of clean_up_dfs:
  This recursive function marks all connected land cells (starting from a border cell) as water (setting the cell value to 0).

  • Base Case:
    The function returns if the cell is out of bounds (x < 0, y < 0, x == len(grid[0]), or y == len(grid)) or if the cell is already water (grid[y][x] == 0).

  • Marking the Cell:
    Once confirmed that the cell is valid and is land, it sets grid[y][x] = 0 to mark it as water.

  • Recursive Calls:
    The function then recursively processes the four adjacent directions: left, right, up, and down. This ensures that any land connected to the border cell is also “sunk”.

• Impact of Cleanup:
  After all border cells and their connected land cells are processed, only the lands that are completely enclosed by water remain.

---

3. Counting the Enclaves

• Iterating Through the Entire Grid:
  After the cleanup, the solution iterates over every cell in the grid.

  • For every cell that is still 1 (land), it increments the counter not_reach_boundary.

• Final Result:
  The variable not_reach_boundary holds the number of enclave land cells, which is then returned.

---

4. Key Points and Complexity

• Depth-First Search (DFS):
  By using DFS, the algorithm can explore and “sink” an entire connected region of land that touches the border in one go. This prevents recounting and ensures that only enclaved regions remain.

• Time Complexity:
  Both the border cleanup and the final counting traverse the grid, leading to a complexity of O(n×m)O(n \times m), where nn is the number of rows and mm is the number of columns.

• Space Complexity:
  The auxiliary space is mainly due to the call stack used in recursion; in the worst case (a very deep recursion), this can also be O(n×m)O(n \times m).

---

Summary

• Step 1: The code eliminates all lands reachable from the boundary using a DFS (clean_up_dfs), effectively “sinking” them.

• Step 2: It then counts the remaining lands, which are the enclaves.

• Result: The count of enclave cells is returned.

This approach is both efficient and elegant as it directly removes irrelevant areas (land connected to the border), leaving a straightforward count of the remaining, fully surrounded cells.